- Home
- /
- 3Dモデリング
- /
- Grasshopper
- /
- 【Grasshopper】実践編 ランダムな曲線空間を作ってみよう
【Grasshopper】実践編 ランダムな曲線空間を作ってみよう

パラメトリックデザインを使ってランダムな空間を作る練習をしてみましょう。
今回は、自由なカーブでできる曲線空間を作っていきます。
この記事を通して、以下のようなモデル↓が出来るようになります!
目次
[PR]
モデリングの流れ
1.円を分割する
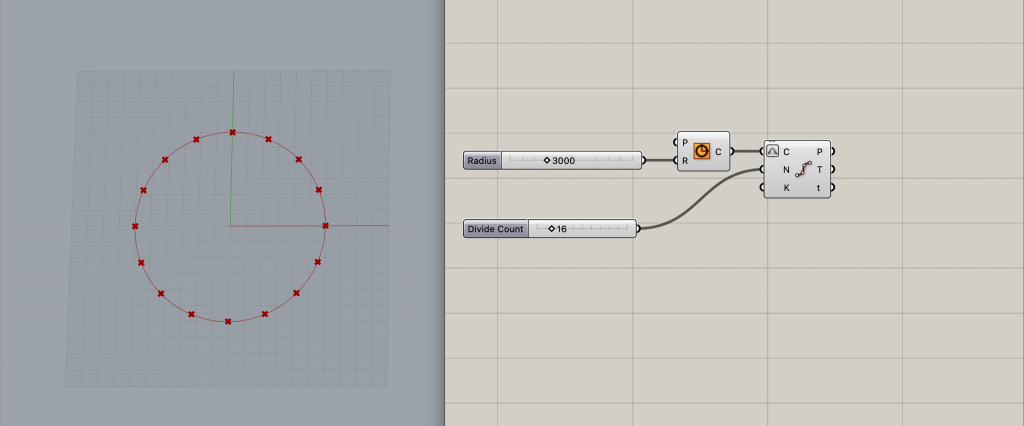
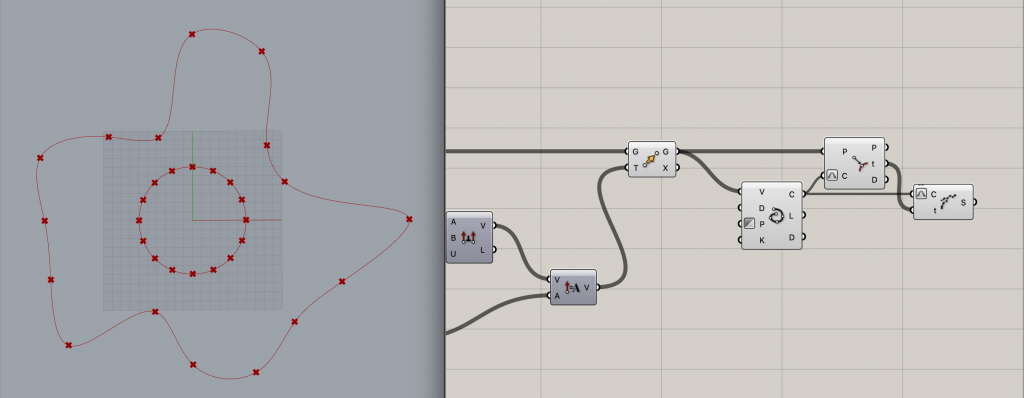
まずは[Circle]コンポーネントで円を作成し、インプットRに3000を代入してみます。
次に[Divide Curve]のインプットCに[Circle]のアウトプットを繋ぎます。
この時、インプットCを右クリックして「Reparameterize」とするようにしましょう。
これは、曲線上の点のパラメータを0から1に再定義すると言う意味なのですが、簡単に言えば
曲線の定義域を0から1に設定し、線の始まりを0、線の終わりを1と決めると言うことです。
こうしておくことで、パラメータtをわかりやすく出力して使用することができます。
そして、[Divide Curve]のインプットNで分割数を指定します。
今回は適当に16としてみました。
ここまでのプログラムは、
「円を16個に等分割する」
という意味になります。
2.法線ベクトルを求める
法線ベクトルを求めるために、外積を利用します。
Grasshopperでは[Cross Product]コンポーネント(外積という意味)を用いて、2つのベクトルに対して直交する方向を持ったベクトルを求めることができます。
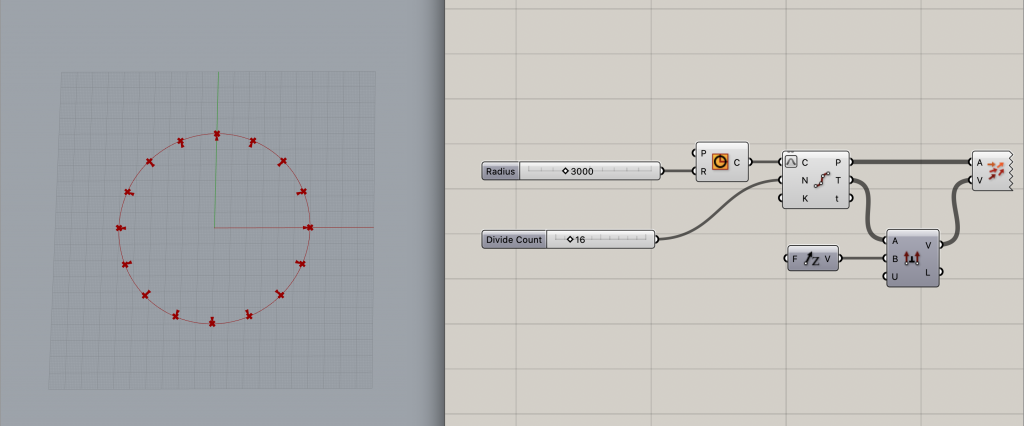
[Cross Product]コンポーネントのインプットAに、[Divide Curve]のアウトプットTを繋ぎます。 [Divide Curve]のアウトプットTからは円に対して接線方向のベクトルが出力されます。
また、[Cross Product]コンポーネントのインプットBに[Unit Z]を繋ぎます。
[Unit Z]はZ軸正の方向を持ったベクトルを意味しています。
つまり、接線方向とZ軸方向に対して直交するベクトルとは、円に対する法線ベクトルを意味しているのです。
よって、ここまでのプログラムは、
「16個の円上の点からそれぞれ法線ベクトルを求める」
という意味になります。
最後に[Vector Display]につなぐことでベクトルをプレビューしてみると以下の画像のようになります。
3.ベクトルの大きさをランダムにする
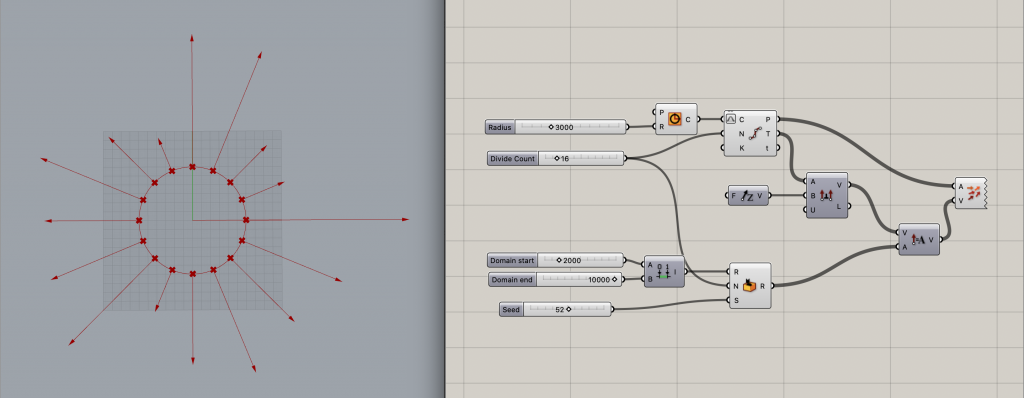
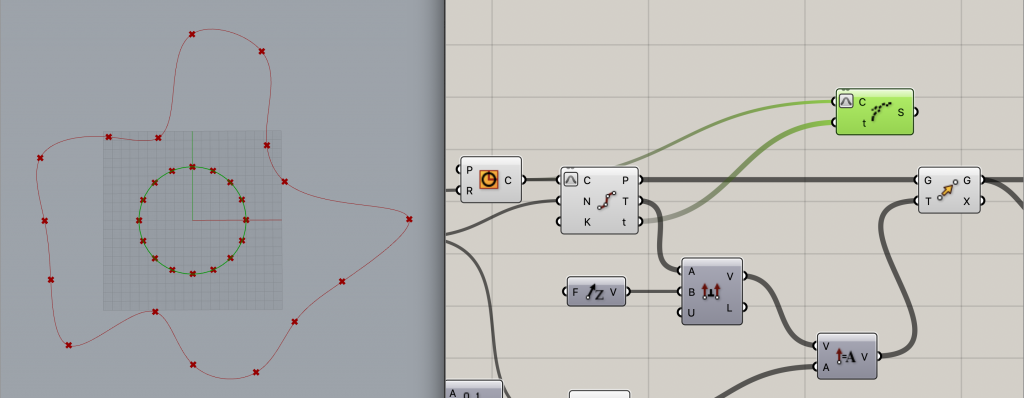
2000、10000に設定した[Number Slider]を[Construct Domain]に接続し、[Random]のインプットRに繋ぎます。
これは、2000から10000の範囲でランダムに数値を出力するという意味になります。
さらに分割数16を指定した[Number Slider]を[Random]のインプットNに繋ぐことで出力数を指定します。
インプットSには適当な数値を代入します。
これはシード値といって、簡単に言うとこの値に応じてランダムな数字を決定するというものです。
そして、この数値の長さを持った法線ベクトルとするために、[Amplitude]コンポーネントを用意します。
[Random]のアウトプットR、[Cross Product]のアウトプットVをそれぞれインプットします。
よって、ここまでのプログラムは、
「16個の法線ベクトルの長さを、2000から10000の範囲でランダムに出力した数値とする」
という意味になります。
最後に[Vector Display]につなぐことでベクトルをプレビューしてみると以下の画像のようになります。
4.外周の曲線を描く
先ほど作ったランダムな16個のベクトルを用いて、円上の点を移動させます。
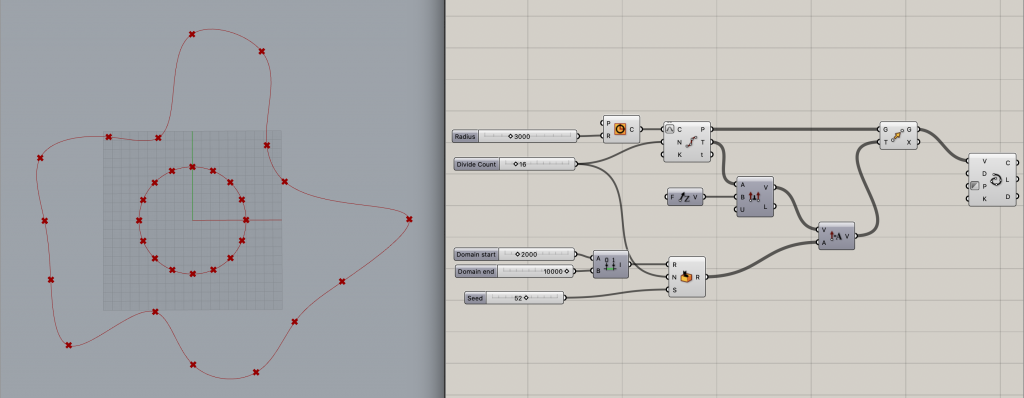
[Move]コンポーネントを用いて点を動かします。また、[Interpolate]のインプットVに接続することで曲線を描くことができます。
この時、インプットPを右クリックし、「Invert」とすることを忘れないでください。
これは、True/Falseを入れ替えるという意味なのですが、初期状態では曲線が閉じずに開いてしまっています。
なのでTrue/Falseを入れ替えて曲線を閉じるようにしましょう。
ここまでのプログラムは、
「ランダムなベクトルで点を移動し、滑らかな曲線でつなぐ」
という意味になります。
5.外側の曲線を分割する
先ほど作った外側の曲線を、曲線上の点を用いて16個に分割したいと思います。
[Move]のアウトプットG、[Interpolate]のアウトプットCをそれぞれ[Curve Closest Point]のインプットP、Cにつなぎます。さらに、[Interpolate]のアウトプットC、[Curve Closest Point]のアウトプットtを[Shatter]のインプットC、tにつなぎます。
この時、[Curve Closest Point]のインプットCと[Shatter]のインプットCはどちらも「Reparameterize」することを忘れないでください。
ここまでのプログラムは、
「外側の曲線を曲線上の点の位置で16分割する」
という意味になります。
6.内側の曲線も分割する
次は同様にして内側の曲線も分割します。
[Shatter]を配置し、インプットC、tにそれぞれ[Circle]のアウトプットC、[Divide Curve]のアウトプットtを繋ぎます。ここでも[Shatter]のインプットCは、「Reparameterize」してください。
ここまでのプログラムは、
「内側の曲線も曲線上の点の位置で16分割する」
という意味になります。
7.さらに分割する
5.と6.の段階で二つの曲線を16分割しました。
次は仕上がりをもっと滑らかにするべく、分割点の間をさらに分割しようと思います。
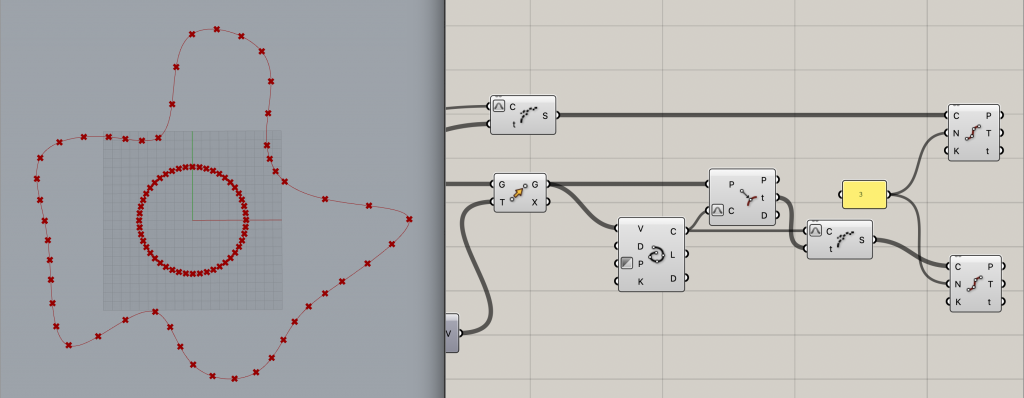
用意するコンポーネントは[Divide Curve]です。1.と同様ですね。
それぞれの曲線を代入するために[Divide Curve]を2つ配置し、曲線をインプットします。
今回は3分割してみようと思うので、3と記述した[Panel]を繋ぎます。
ここまでのプログラムは、
「内側と外側の曲線それぞれにおいて、分割点の間を3分割する」
という意味になります。
8.線で結ぶ
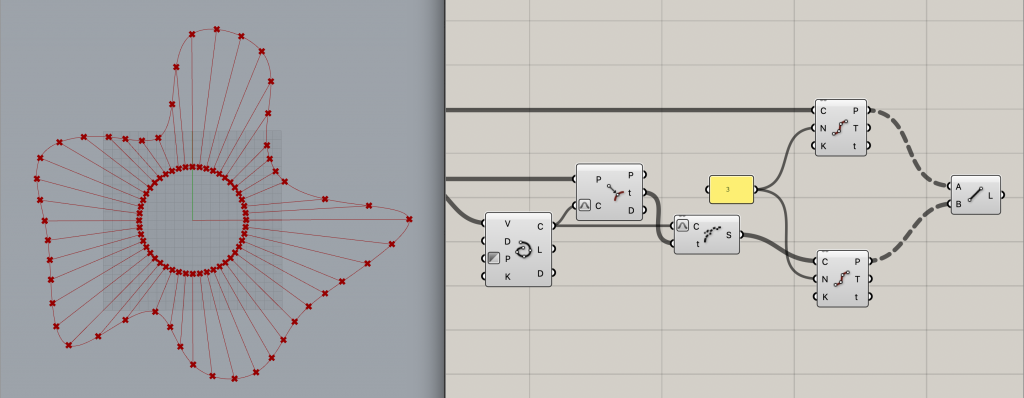
たくさん分割してきましたが、ここで、内側の分割点と外側の分割点を直線で結んであげようと思います。
2つの[Divide Curve]のアウトプットPをそれぞれ[Line]にインプットしましょう。
このプログラムは、
「それぞれの分割点を直線で結ぶ」
という意味になります。
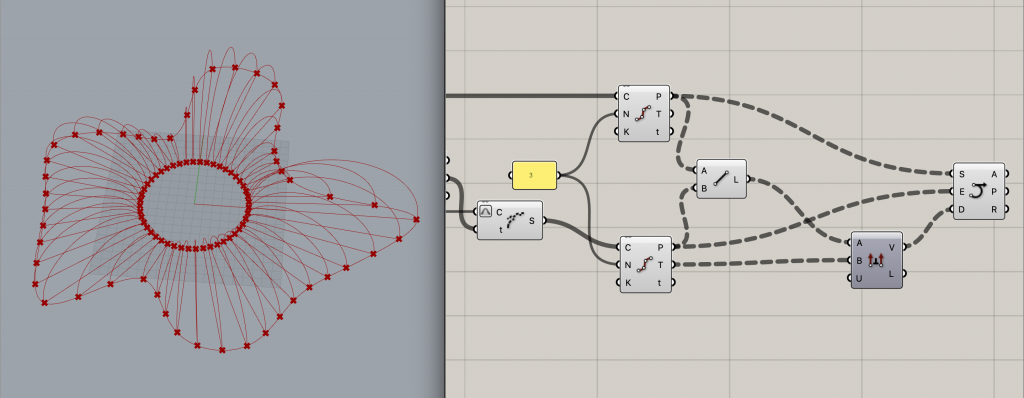
9.円弧を描く
先ほど作成した線の上に、円弧を描いていきましょう。
最終的な曲線の壁面を形成する骨のような役割です。
円弧の作成には[Arc SED]というコンポーネントを使用します。
Arc とは曲線のことで、 SED とはそれぞれStart、End、Directionの頭文字を表しています。
つまり、始点・終点・接線方向を指定することで円弧を定義すると言う意味です。
ここで始点と終点はそれぞれ曲線上の分割点を指定すれば良いので、インプットに繋げるだけです。
問題は接線方向。
円弧が始点から終点に向かうまでの接線方向ベクトルを作成する必要があります。
勘が良い人はお気づきかと思います。そうです、またまた外積を利用します。
先ほど8.で作成した線の方向ベクトルと、分割点における接線方向ベクトルについて直交するベクトルを[Cross Product]で求め、[Arc SED]のインプットDに繋ぎます。
このプログラムは、
「分割点同士をつなぐ円弧を作成する」
という意味になります。
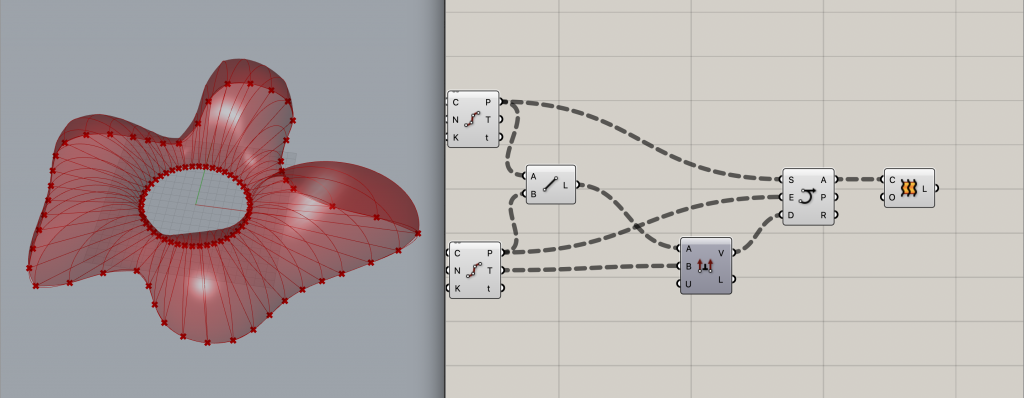
10.滑らかな面を作成し、完成!
先ほど作成した円弧を元に、滑らかな曲面サーフェスを作成します。
コマンドは簡単で、[Arc SED]のアウトプットAを[Loft]のインプットCにつなぐだけです。
このプログラムは、
「円弧を元にサーフェスを作成する」
という意味になります。
これで曲線空間が出来上がりました。
[求人情報]
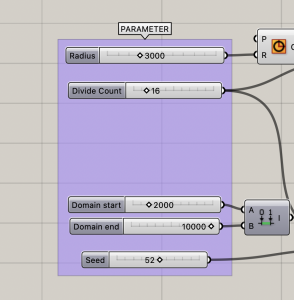
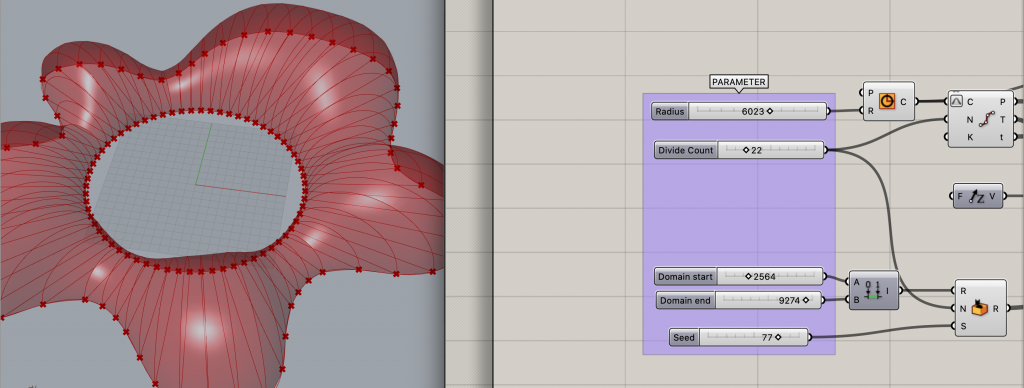
変数をいじってみる
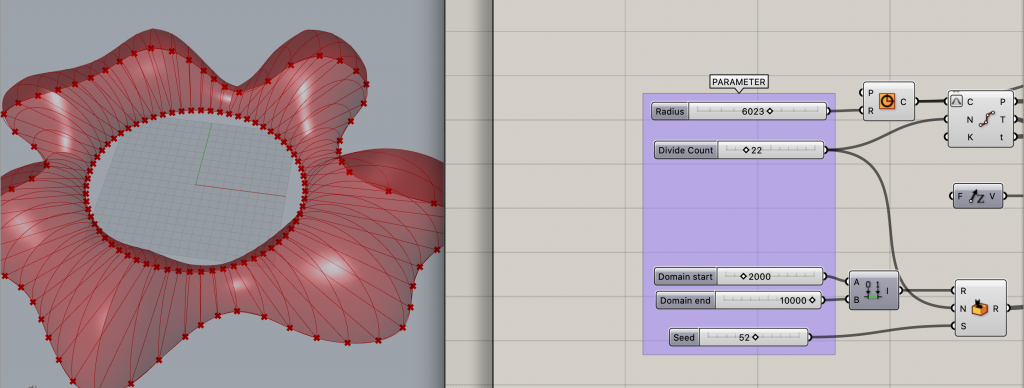
完成したモデルの[Number Slider]コンポーネントを自由にいじってみましょう。
円の半径を大きくして、分割点を多くしてみたり…
ランダムな幅の範囲を狭めてみたり、シード値を変えてみたり…
それぞれが指定した数値に応じて柔軟に対応していることが確認できます。
自在にいじって比較してみましょう!
参考書
今回のモデルは、以下の書籍を参考にしながら若干の変化を加えて解説しました。
わかりやすいので是非手にとってみてくださいね。
最後に
いかがだったでしょうか。
今回は自由なカーブでできるランダムな曲線空間を作ってみました。
パラメーターによって空間が変化する様子を楽しみつつ、比較検討してみてください!
それでは。